Blinn-Phong

So turns out Jim Blinn tweaked Phong’s shading so it would be more efficient, which gave us the Blinn-Phong model we all know and love today.

Instead of calculating viewDir · reflectionDir per frame, as we did before, Jim uses a half-vector viewDir + lightDir and compares that with the normals of the fragment.

Since the normals are calculated in the vertex pass, they are calculated once for N fragments. It saves us the reflect(L, N) call per fragment, which is nice.

void main() 
{
    vec3 N = normalize(fragNormal);
    vec3 L = normalize(lightDir);

    vec3 viewDir = normalize(viewPos - fragPosition);
    
    // Predefined light directions, like sunlight, need to be inverted
    vec3 halfVector = normalize(-L + viewDir);
    float onlySpecular = max(0, dot(halfVector, N));

    vec3 specular = specularTint * pow(onlySpecular, smoothness * 100);

    finalColor = vec4(specular, fragColor.a);
}

Plus, it also makes elliptical speculars possible when viewed at a steep angle, which is more realistic! A classic win/win situation.

To make those just a tad more realistic, we are going to darken the albedo in relation to the specular tint, to simulate glossiness:

And here is our park again, a comparison between the two:

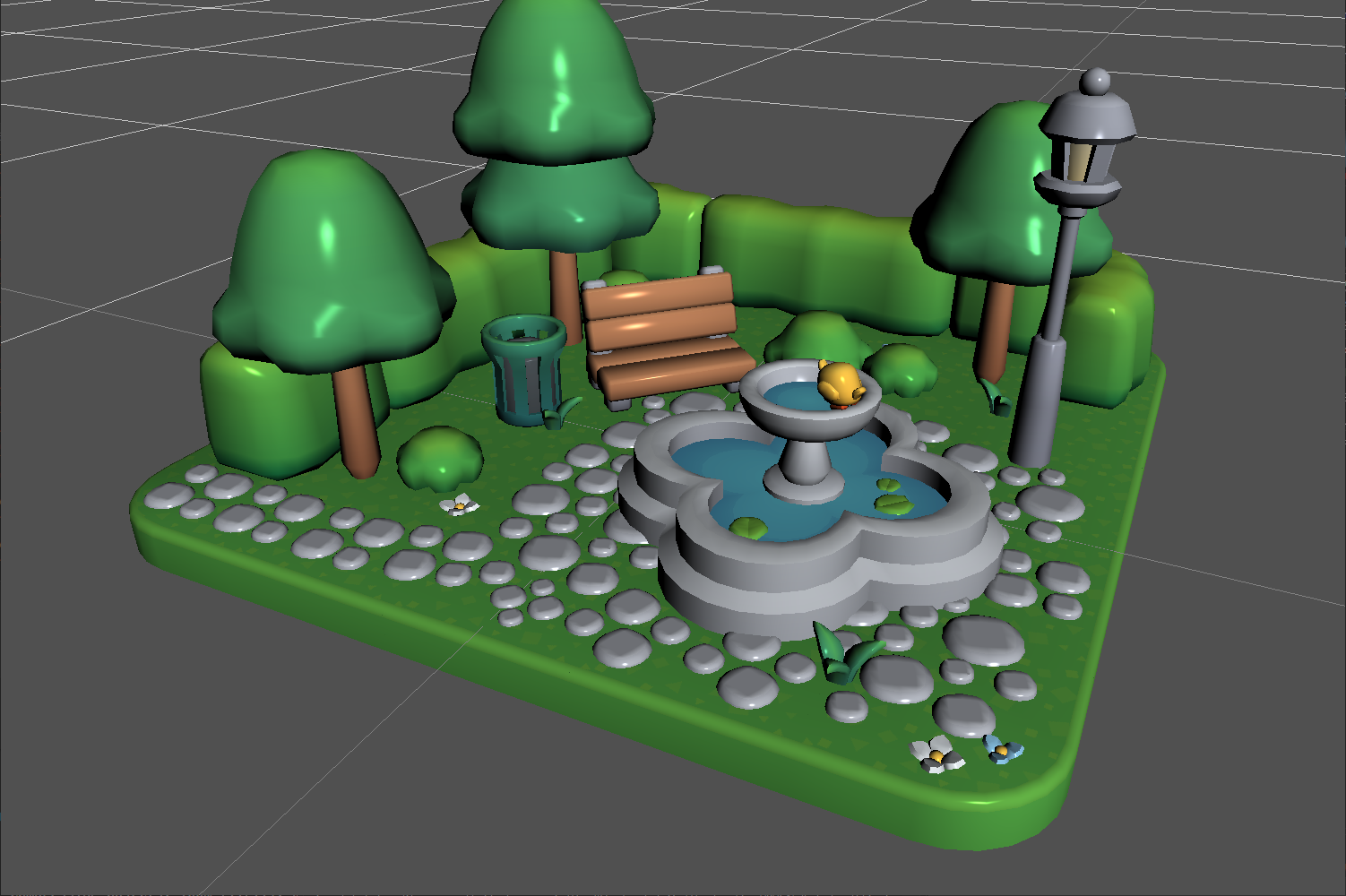
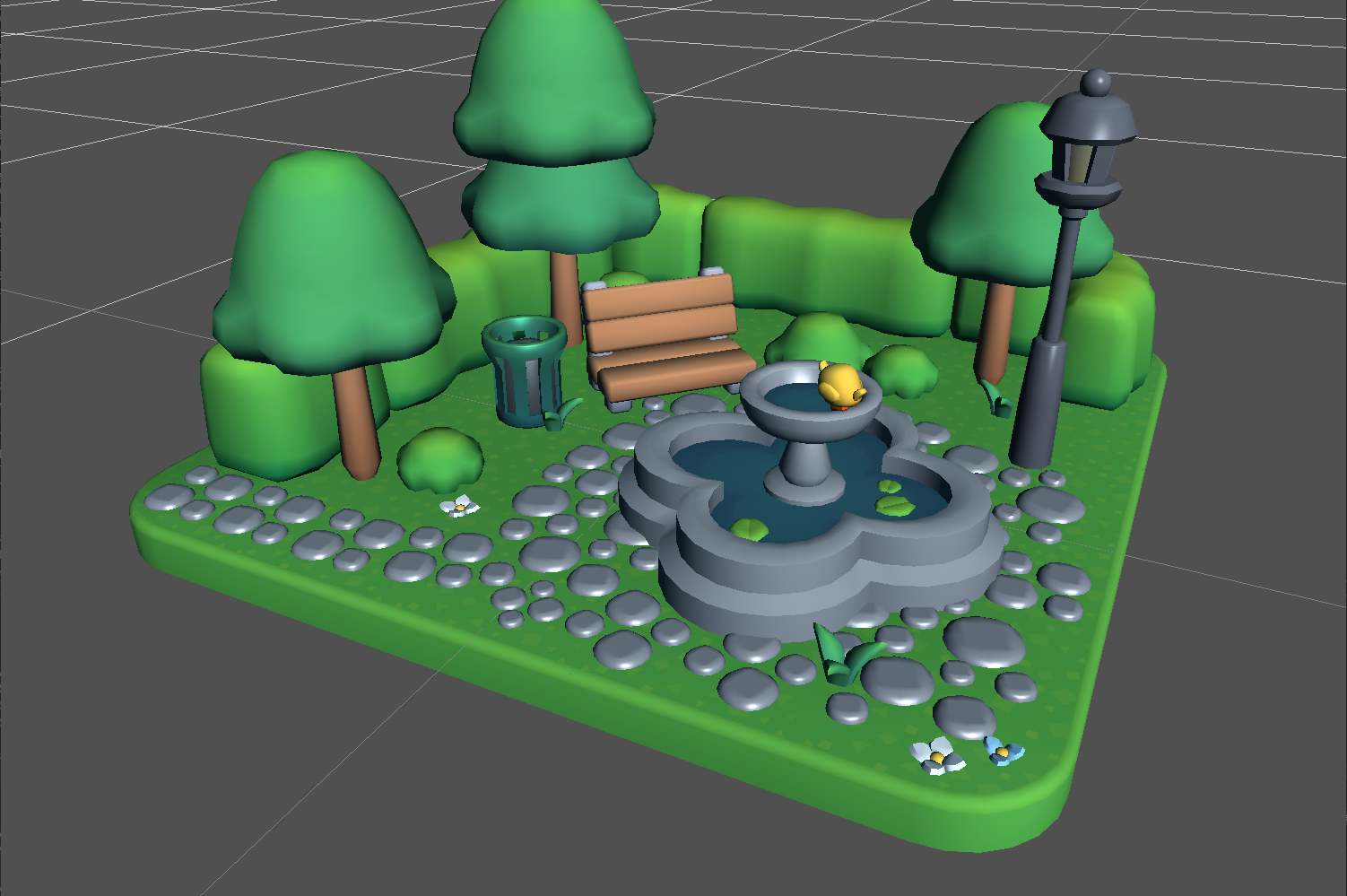
The most noticeable differences are the fountain and the cobblestones.